Penetration Depth

The fluorescence radiation for an element is absorbed as it leaves the sample. Beginning with a certain depth in the sample, the fluorescence signal is completely absorbed, i.e., all atoms that lie deeper than this can no longer be analyzed, as the radiation can no longer reach the surface.  This depth is called the penetration depth or the infinite thickness.

The penetration depth increases with the atomic number. It is independent from the XRF instrument used, the excitation voltage or current from the X-ray tube. It is determined exclusively by the sample matrix.

Figure 34 clearly shows that an observed element is only analyzed in a layer up to the maximum penetration depth.

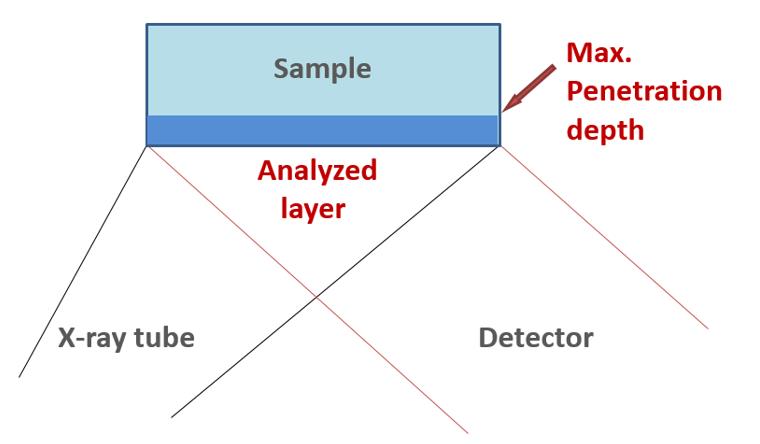
Formula (15) can be used to calculate the penetration depth. It can be derived from formulas (3) and (14). In formula (3), the linear absorption coefficient, µ_lin, is replaced by the mass absorption coefficient, µ. In this way, the density, r, of the total sample is introduced into the formula.

In addition, it is assumed that after absorption along the distance, h, a residual intensity of 0.1% remains. The mass absorption coefficients for every fluorescence line and for every pure element matrix are listed in tables [23].

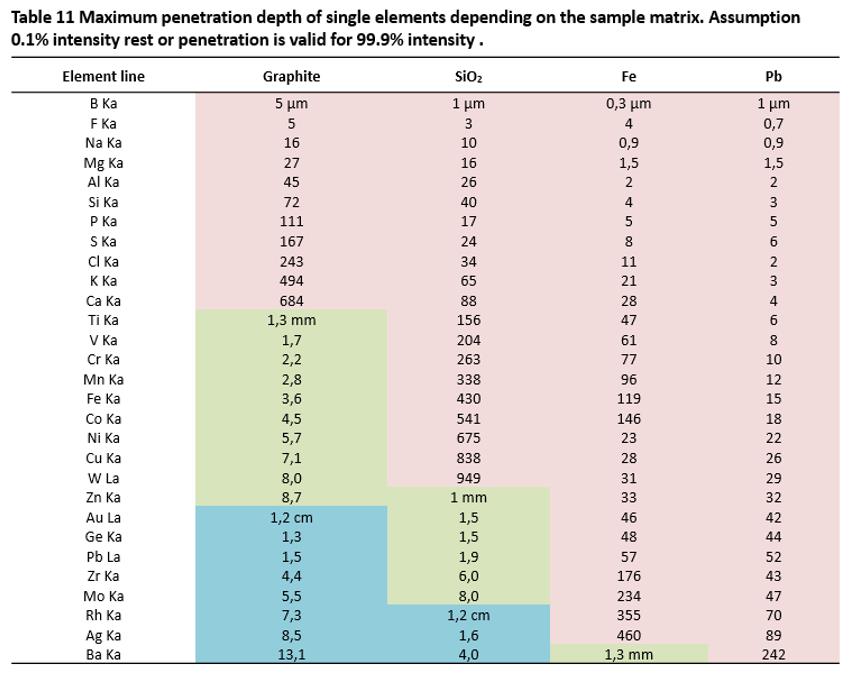
The vertical penetration depths for a selection of elements in various matrices are calculated in Table 11.

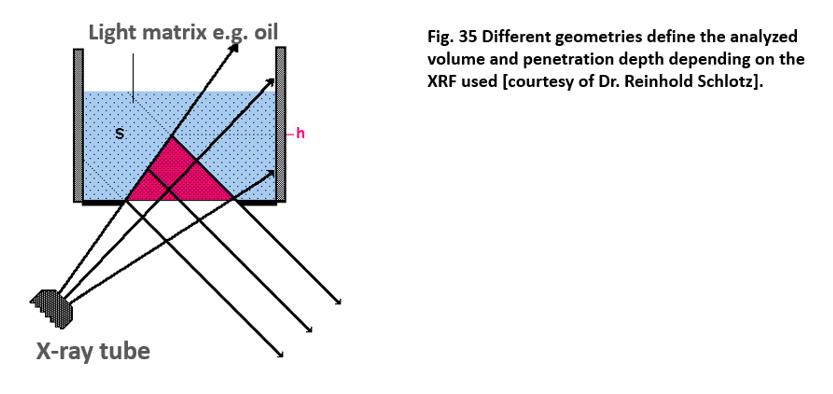
The geometry of the excitation and the detection must be taken into consideration. Because the detection is usually performed with a given angle (e.g., 45°), the vertical penetration depth is reduced (Fig. 35).

The fill height plays a role in light matrices, such as oil. Even when it is higher than the maximum penetration depth for the given element, a change can influence the course of the background. One reason for this is that the excitation radiation penetrates deeper due to its higher energy. Another reason is that more multiple scattering occurs in light matrices.